Probabilistic Neural Network |
| A probabilistic neural network (PNN) can be seen as a statistical method or an artificial neural network. The mathematical background of PNN was ready before ANNs were known. However, back then, computers did not have enough power so that PNN algorithms could be used. In 1990, Donald Specht proposed a method that could break down the computations of the algorithm. As these neural networks were born because of probability theory, they are called probabilistic neural networks. |
Training Set |
| As before, PNNs are trained using a data set called training set. This training set has two parts: the input and the target. The figures below shows the training set input and the training set target. Both parts of the training set have the same number of rows, N, or cases. The number of columns in the training set input must be equal to the number of inputs in the PNN. The number of columns in the training set target must be equal to the the number of outputs in the PNN. Thus, the training set below can be used on a PNN with λ inputs and μ outputs. |


PNN Structure |
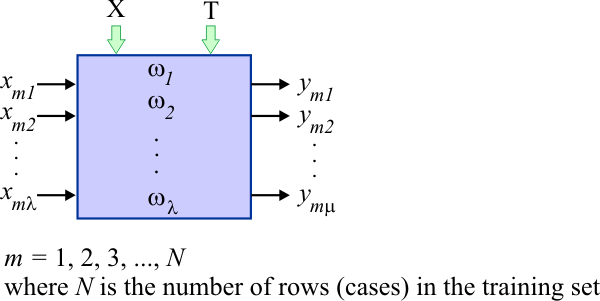
| The figure below shows the structure of a PNN with λ weights. A PNN has a weight for each input. In general, a PNN has fewer weights than an ANN. The PNN of the figure has λ inputs and μ outputs. The figure illustrates the output of the PNN when the m training case is applied to the input of the network. An ANN requires the training set input and the training set target during the training of the network. Once an ANN has been trained, an ANN does not require the training set to operate. On the other hand, a PNN requires the training set for training and normal operation. This is indicated in the figure by the green arrows on the top of the PNN. Thus, a PNN requires more memory and computation than an ANN for normal operation. One of the main advantages of PNNs is that (when there are few training cases) they can be trained faster than ANNs. Additionally, because PNNs are based on probability, it is easier to predict their behavior. |
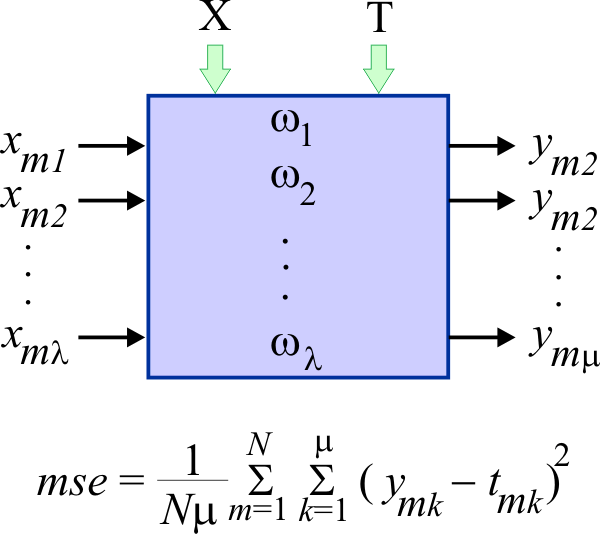
Mean squared error (mse) |
| The mean squared error is used to assess the quality of the training of a PNN. The figure below illustrates how the mse is computed. From the equation, it can be seen that the mse is computed between the actual output of the PNN and the training set target for all cases in the training set. |